Abschlussfeier 2025 am 7. November 2025 in Hörsaal 33
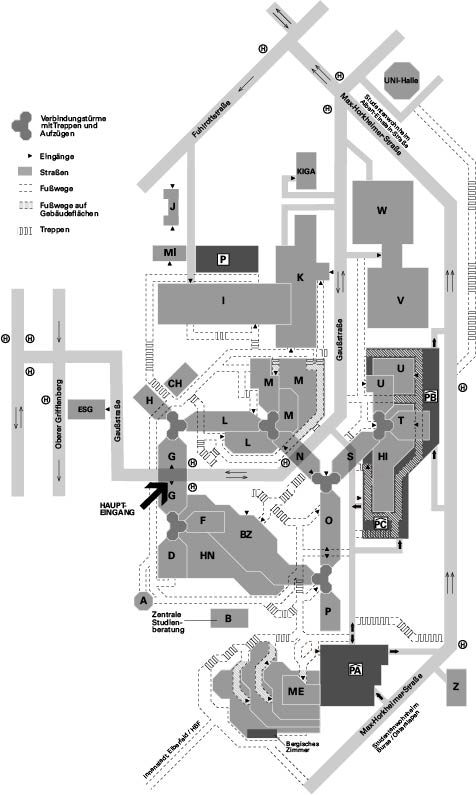
Unserer Abschlussfeier findet wie auch in den letzten Jahren im Hörsaal 33 und Foyer Gebäude K statt.
Ablauf
15:30 Einlass (Möglichkeit ein Foto im Talar machen zu lassen)
16:30 Fototermin (Gruppenfoto aller Absolvent*innen)
16:40 Fototermin (Gruppenfoto der Preisträger*innen)
17:00 Beginn der Veranstaltung
Eröffnung durch den Dekan, Prof. Dr. Francesco Knechtli und die Rektorin, Prof. Dr. Birgitta Wolff
Als Gastredner wird Herr Dr. Arne Lawrenz, Direktor des Grünen Zoos Wuppertal, den Festvortrag mit dem Titel „Moderne Zoos und ihre Aufgaben – Fokus Forschung“ halten.
Anschließend erfolgt die Ehrung der Absolventinnen und Absolventen und die Vergabe der BarmeniaGothaer-Mathematikpreise, und verschiedener anderer Preise.
ca. 19:50 - 22:00 Sektempfang und Flying Food gesponsert von der BarmeniaGothaer
Weitere wichtige Hinweise zum Ablauf der Ehrung
Für die Ehrung werden alle teilnehmenden Absolventinnen und Absolventen einzeln und namentlich aufgerufen. Um einen reibungslosen Ablauf zu gewährleisten, bitten wir Sie, sich bereits jetzt zu informieren, welcher Laufgruppe Sie zugeordnet sind. Werfen Sie dazu bitte einen Blick auf die Lauflisten der Teilnehmenden. Dort finden Sie die letzten vier Ziffern Ihrer Matrikelnummer.
Laufliste der Teilnehmenden
Bitte werfen Sie auch einen Blick auf den Laufplan für Hörsaal 33.
Laufplan
Am Donnerstag oder Freitagmorgen wird außerdem noch der Sitzplan für die verschiedenen Gruppen auf dieser Webseite hochgeladen.
Wenn Sie mit dem Auto anreisen, können Sie in Parkhaus A oder C parken (siehe Lageplan Grifflenberg). Beide Parkhäuser bleiben bis 22:30 Uhr geöffnet.
Sollten Sie kurzfristig erkranken oder anderweitig verhindert sein, senden Sie bitte eine kurze Nachricht an alumnifk4(at)uni-wuppertal.de, damit wir Sie von der Liste entfernen können.
FAQ
Sie können bis zu zwei Gäste zur Abschlussfeier mitbringen. Bitte geben Sie im Anmeldeformular insgesamt drei Personen an (Ihre eigene Anmeldung plus die Ihrer beiden Gäste).
Als Absolvent*in erhalten Sie bei Teilnahme an unserer Abschlussfeier eine von der BarmeniaGothaer gesponserte Freikarte der Kategorie "Flanierkarte" für den abendlichen Ball am nächsten Tag (Samstag 8.11.). Bitte geben Sie bei Ihrer Anmeldung zur Abschlussfeier an, ob Sie Ihre Freikarte für den Ball in Anspruch nehmen möchten. Ihre Freikarte wird dann für Sie reserviert. Die Freikarte ist personalisiert und kann somit nicht auf andere Personen übertragen werden. Wenn Sie nicht an der Abschlussfeier teilnehmen oder trotz Anmeldung nicht erscheinen, erlischt der Anspruch auf Ihre Freikarte. Ggf. bereits aktivierte Freikarten werden dann wieder storniert.
Die Koordination der Uniballkarten geschieht nicht über die Fakultäten, sondern über die zentrale Alumnistelle der BUW.
Wenn Sie Ihre Freikarte in Anspruch nehmen, haben Sie außerdem die Möglichkeit, noch weitere Flanierkarten aus dem Begleitkartenkontingent zu erwerben. Beide Kontingente werden Mitte Oktober freigeschaltet. Sie erhalten dann in einer E-Mail alle Infos zur Freischaltung, die Ticketshop-Zugänge und den Aktivierungscode für Ihre Freikarte. Hier können Sie dann einmal Ihre Freikarte aktivieren und zum anderen die Begleitkarten käuflich erwerben.
Bitte beachten Sie: Das Kontingent an Begleitkarten enthält ausschließlich Karten der Kategorie „Flanierkarte“ (35 € pro Karte zzgl. VVK-Gebühr) und ist limitiert: Pro Absolvent*in stehen maximal zwei Begleitkarten zur Verfügung, solange Vorrat reicht. Wenn Sie nicht an der Abschlussfeier teilnehmen oder trotz Anmeldung nicht erscheinen, erlischt der Anspruch auf Ihre Freikarte. Bereits aktivierte Freikarten werden dann wieder storniert.
Bleiben Sie mit uns in Kontakt!
Wir würden uns freuen, wenn Sie als ehemalige Student*innen, Absolvent*innen und Mitarbeiter*innen der Fakultät für Mathematik und Naturwissenschaften mit uns in Kontakt bleiben. Eine Möglichkeit ist zum Beispiel über eine Mitgliedschaft in unserem Verein zur Förderung von Mathematik & Naturwissenschaften e.V.
Treten Sie auch dem Alumni-Netzwerk der Bergischen Universität bei, um weiterhin Neuigkeiten aus der Uni und Einladungen zu interessanten Veranstaltungen zu erhalten.
Verein zur Förderung von Mathematik und Naturwissenschaften e.V.
Bilder: https://www.malte-reiter.de/
